L’entrada d’avui correspon a les unitats didàctiques 2 i 3 de l’assignatura (cinemàtica lineal i angular, respectivament). Ja que la temàtica està relacionada, i per tal de reduir una mica el nombre d’entrades, m’ha semblat més adient juntar-les en una de sola.
Nota
Com ja sabeu, totes les entrades de la secció apunts del Grau en Nutrició Humana i Dietètica i Ciencies de l’Activitat Física i l’Esport estan extretes del material proporcionat per la Universitat Isabel I de Castilla. A més, en aquesta assignatura en particular, hi ha una bona feina de redacció per part de l’equip docent que la coordina. Els corresponents crèdits, doncs, a la universitat i a l’equip. La meva missió aquí només és traduir-los i aportar alguns enllaços extra com a material addicional.
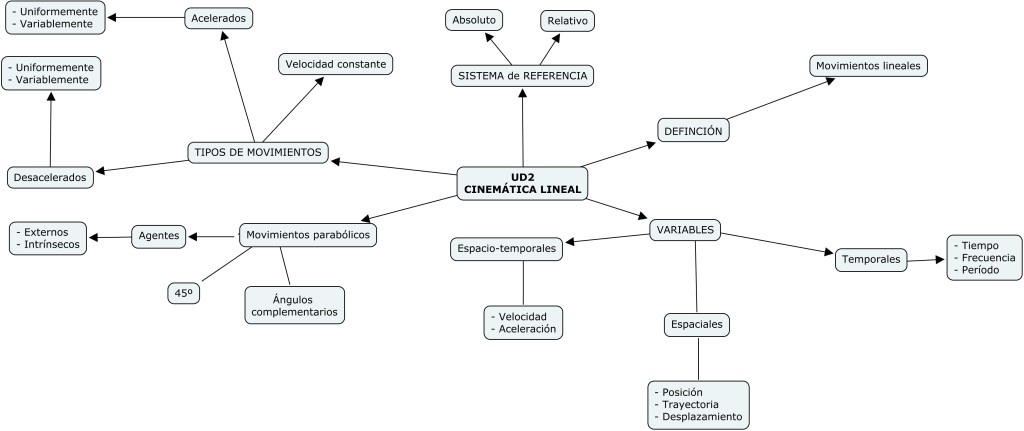
Cinemàtica lineal
La biomecànica esportiva té un camp d’actuació molt important en l’estudi i l’observació dels moviments, així com en la interpretació dels esforços requerits per a la seva execució. Fruit d’aquest tipus d’estudi, se sol treballar amb variables quantitatives que ajuden a interpretar i perfeccionar la tècnica esportiva.
En aquesta unitat didàctica s’estudiaran les diverses variables específiques de la cinemàtica lineal aplicades a casos reals de l’activitat esportiva. Aquestes variables estan agrupades en tres sectors ben diferenciats: temporals, espacials i espai-temporals.
Aproximació al concepte de cinemàtica lineal
Tal com s’indicava en la unitat anterior (UD1), la cinemàtica és la part de la física que estudia les lleis del moviment dels cossos, però sense analitzar les causes que el provoquen. La cinemàtica lineal estudia aquells moviments de tipus lineal i parabòlic.
Però, què entenem per moviment? La Reial Acadèmia de la Llengua defineix en la seva segona accepció de moviment com el “estat dels cossos mentre canvien de lloc o de posició”. Des del punt de vista de la física, el moviment es descriu com la variació de posició que experimenta un cos en un període de temps respecte a un sistema de referència fix (o que es considera com a tal).
En biomecànica, per analitzar el moviment no només s’estudia el canvi de posició d’un cos en la seva globalitat, pot ser també el del seu centre de gravetat o d’una de les seves parts. En aquests casos se sol col·locar marcadors en punts anatòmics de referència. Però el concepte de cos és més ampli, comprèn també materials esportius (canoa, bicicletes), implements (raquetes, pals de golf) o objectes com pilotes, fletxes o pilotes.
Aprèn més
En aquest punt caldria revisar, si no s’hi està familiaritzat, els punts anatòmics de referència, vists a l’assignatura de cinesiologia (però que no estan al blog). Aquest enllaç us pot ser útil 😉

Exemple de marcadors corporals per a anàlisi biomecànic.
Variables de la cinemàtica lineal
Les podem dividir en variables temporals, espacials i espai-temporals. Anem a veure cadascuna d’elles.
Variables temporals
El temps és la primera i principal variable d’aquest apartat. Segons la Real Acadèmia de la Llengua, temps es defineix com la magnitud física que permet ordenar la seqüència dels successos, establint un passat, un present i un futur. La seva unitat en el Sistema Internacional és el segon.
A partir del temps s’arriba a la segona variable, la freqüència. Segons la Real Acadèmia de la Llengua, freqüència és el nombre de vegades que es repeteix un procés periòdic per unitat de temps. El nombre de pulsacions per segon, el nombre de gambades o braçades, són variables de freqüència molt usades en l’àmbit esportiu. En el sistema internacional la freqüència es representa per una lletra f minúscula.
En funció de la freqüència s’obté la tercera variable temporal, el període. Segons la Real Acadèmia de la Llengua, període és l’espai de temps que inclou tota la durada d’alguna cosa. És el temps que fa falta per realitzar un moviment i es calcula amb l’invers de la freqüència. Es representa per una p minúscula.
Exemple pràctic
En una cursa de 400 m tanques, Edwin Moses triga a recórrer els 35 m de distància entre la tanca vuitena i novena 3,80 s durant els quals efectua 13 gambades. La seva freqüència de gambada en aquest tram serà de 3,42 gambades per segon.
![]()
A través d’aquesta dada podem obtenir la informació sobre el període de temps que triga a efectuar una gambada, que serà de 0,29 s.
![]()
Variables espacials
Les variables espacials fan referència al canvi de posició en l’espai que registra un cos, objecte, o segment d’aquest, respecte a un punt de referència considerat fix. Aquest canvi de lloc està vinculat al temps que es requereix per efectuar aquest desplaçament.
La posició d’un cos fa referència a la seva localització en l’espai en relació sempre a un punt de referència, que es considera com a fix. Per exemple, si es diu que l’altura d’una tanca per a una carrera de 400 m ha d’estar a 0,914 m, vol dir que aquesta és l’altura respecte al terra, que és el sistema de referència fix i està a l’altura 0 m.

L’alçada de la tanca varia en funció de la carrera i la categoria. Per exemple, en 400 m seria de 0,914 m per a homes i 0,762 per a dones. En els 110 m tanques masculins estaria a 1,0667 mi en els 100 m tanques femenins l’altura seria de 0,898 m.
Però la posició també pot estar representada per un vector, anomenat vector posició. Aquest seria el vector traçat des de l’origen del sistema de referència fix, o coordenades, fins a la posició del cos.
La segona variable a estudiar és la trajectòria, que té caràcter escalar, no vectorial, i fa referència a la longitud del camí recorregut per un cos durant cert interval de temps.
El vector desplaçament es refereix a la diferència de posició d’un cos al llarg del temps. El desplaçament té caràcter vectorial, i seria el vector resultant que uniria la posició inicial i la posició final. La unitat de mesura internacional per la trajectòria i el desplaçament és el m (Arteaga, 2008).
Nota
Quan un corredor dóna una volta en una pista d’atletisme, la trajectòria recorreguda seria de 400 m però el desplaçament seria zero perquè el seu punt inicial i final serien el mateix.
Variables espai-temporals
Les variables espai-temporals relacionen la variació d’un cos al llarg de l’espai amb el temps emprat. Les dues variables espai-temporals són la velocitat i l’acceleració.
La velocitat té caràcter vectorial. El diccionari de la RAE defineix velocitat com la magnitud física que expressa l’espai recorregut per un mòbil en la unitat de temps. Des del punt de vista de la física, el vector velocitat es defineix com la variació de la posició per l’interval de temps (Tipler, 2000).

Imatge de David Rudisha
Si apliquem aquesta fórmula a una realitat esportiva, per exemple quan David Rudisha va batre el 2012 el rècord del món de 800 m, va establir una marca de 1’40.91 s el que significa que va córrer a una velocitat de 7.92 m/s.
Aquesta és la velocitat mitjana desenvolupada per l’atleta, però al llarg del recorregut la velocitat no va ser constant, sinó que va variar en funció de cada part del trajecte. Si es prengués com a referència diferents intervals de la cursa tindríem resultats més precisos de les velocitats parcials al llarg del recorregut.
Nota
Per a calcular la velocitat en aquest cas, s’ha de començar transformant el temps en segons. Així, 1’40.91 és el mateix que 1 minut i 40.91 s, o el que és el mateix, 60 + 40.91 segons, en total 100.91 s. Posteriorment es procedeix a dividir la distància de 800 metres entre el temps, obtenint com a resultat 7.92 s.
Igual que en el cas de la cursa de 800 m, a la vida real no se sol registrar velocitats constants, sinó que varien al llarg dels diferents períodes del seu desplaçament. En aquests casos sorgeix una segona variable derivada de la velocitats que s’anomena acceleració. Segons la RAE, l’acceleració és la magnitud que expressa l’increment de la velocitat en la unitat de temps.
És a dir, quan un cos augmenta la seva velocitat s’aprecia una acceleració, i quan la disminueix pateix una desacceleració (Arteaga, 2008).
L’acceleració s’expressa per la següent fórmula:
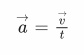
Des del punt de vista de la física, el vector acceleració es defineix com la variació de la velocitat per l’interval de temps (Tipler, 2000).
![]()

En una carrera de motociclisme els pilots acceleren les seves motos a les rectes i desacceleren abans de les corbes.
Tipus de moviments segons les relacions entre espai i temps
En funció de la velocitat i l’acceleració d’un cos podem trobar diferents tipus de moviments. En primer lloc trobem moviments a velocitat constant, o aquells que recorren una mateixa distància en el mateix període de temps. A la vida real és difícil que es doni, pot trobar-se en ciclistes que són capaços de mantenir una velocitat constant gràcies a les indicacions del velocímetre.
Els moviments accelerats serien aquells en què la velocitat no és constant sinó que augmenta gradualment. Per contra, els moviments desaccelerats serien els de frenada, aquells en què la velocitat disminueix.
Però aquesta variació de velocitat pot ser constant o variable. D’aquesta forma trobem moviments uniformement accelerats quan la velocitat s’incrementa de forma constant. Un exemple seria quan es deixa caure d’un trampolí a la piscina. El CDG de l’individu acceleraria de manera constant en funció de la força de la gravetat a una velocitat de 9.8 m/s cada s.

En saltar al mar des d’una alçada determinada, la força de la gravetat fa que la velocitat augmenti 9.8 m/s cada segon, és a dir, accelera a 9.8 m/s2
Seria uniformement desaccelerat quan la velocitat es redueix de forma constant al llarg del temps. Per exemple si realitzem un salt vertical, després d’enlairar els peus de terra el CDG redueix la seva velocitat de forma constant, desaccelerant a 9.8 m/s 2 .
Més comuns són els moviments amb una acceleració variable. Així trobem moviments variablement accelerats, que serien aquells en què a mesura que transcorre el temps la velocitat augmenta, per exemple a la sortida d’una cursa de 400 m tanques. L’atleta passa d’estar aturat a augmentar la velocitat progressivament. Finalment es parla de moviments variablement desaccelerats quan es redueix la velocitat al llarg del temps però no de forma constant. Per exemple quan s’arriba a la meta en una cursa de 100 mi es frena per aturar.
Sabies que…
La força de la gravetat és un vector que té una direcció perpendicular a la superfície terrestre i sentit cap al centre de la Terra. L’acceleració d’aquesta força té un valor registrat d’9.8 m/s2 a nivell del mar en el paral·lel 45º.
Cinemàtica lineal i biomecànica esportiva
La unitat planteja un exemple que aquests conceptes en forma de taula i que obviaré, ja que ens suggereix una altra lectura interessant sobre els parcials d’Usain Bolt als 100m, més vistosa i suficient, que hi ha molt temari!
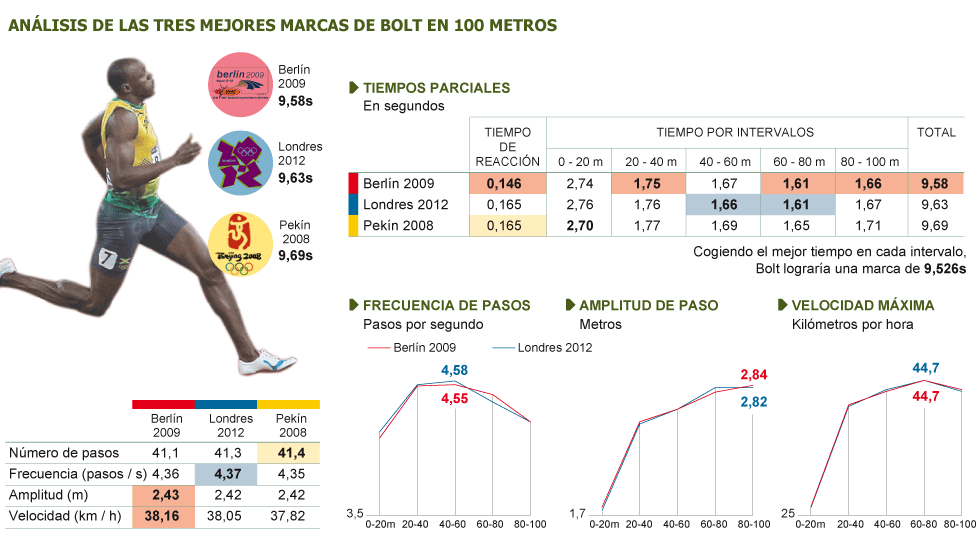
La imatge mostra alguns dels conceptes estudiats com els temps parcials (taula superior-dreta) la freqüència i la velocitat (taula inferior-esquerra) i l’acceleració i desacceleració (gràfiques inferiors-dreta).
Moviments parabòlics
S’anomena moviment parabòlic a la trajectòria d’un objecte que descriu una paràbola en la seva fase aèria. És un moviment molt comú en l’àmbit esportiu i d’especial atenció en la biomecànica esportiva. Una pilota de bàsquet en un tir lliure, la javelina o un saltador de longitud són alguns dels exemples de trajectòries parabòliques en l’esport.
El moviment parabòlic consisteix en un cos que és llençat o impulsat a l’aire amb una component horitzontal i que es deixa moure lliurement (Tipler, 2000). El moviment d’aquest cos estarà condicionat per dos tipus d’agents:
- Externs al sistema, com són la força de la gravetat i la resistència a l’aire
- Intrínsecs al sistema: la velocitat inicial i l’angle de sortida respecte a l’horitzontal
Sempre que en la fase aèria no influeixin corrents d’aire ni forces de sustentació que modifiquin la trajectòria, els cossos llançats amb alguna component horitzontal realitzaran una paràbola perfecta.
L’acceleració gravitatòria condicionarà la trajectòria parabòlica de dues formes: desaccelerant la component vertical de l’objecte cap amunt fins que aconsegueixi l’altura màxima, o bé accelerant l’objecte cap avall fins que impacti amb el terra.
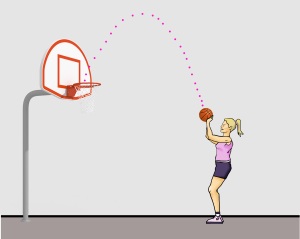
Descripció de la trajectòria parabòlica d’una pilota de bàsquet en el seu recorregut a la cistella.
En funció de l’angle i la velocitat de llançament s’arribarà a una distància determinada. De manera que coneixent aquestes dades i la posició de sortida, és possible estimar el punt d’arribada (Aguado, 1993).
La fórmula per a estimar la distància assolida seria la següent:
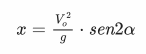
Si es multiplica divideix per 2 la part dreta de la fórmula anterior, es pot trobar la component y del moviment, és a dir, l’alçada.
D’aquestes dues fórmules podem extraure una gran conclusió referent al grau òptim per assolir la màxima distància. Per això n’hi ha prou amb buscar l’angle per tal que el seu sinus obtingui el màxim valor. L’angle que possibilita una distància més llunyana és el de 45º, ja que el sinus de 45º és 1, i per tant el major valor possible (recordem que va de 0 a 1). En canvi, per a aconseguir la màxima alçada, l’angle de sortida haurà de ser de 90º (i per això el 2 de la segona fórmula, 90/2 = 45).
Un altre aspecte important pel que fa als graus de sortida és el dels angles complementaris. Angles que sumin 90º arribaran a la mateixa longitud. Així, un objecte llançat a 60º i a 30º arribaran igual de lluny sempre que parteixin amb la mateixa velocitat inicial (Aguado, 1993).
La següent imatge mostra de manera més intuïtiva els conceptes anteriors. Analitzant-la una mica, resulta força evident per sentit comú.
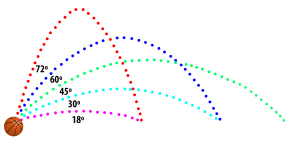
Descripció de la trajectòria parabòlica d’un objecte amb angles complementaris.
Existeixen 3 possibilitats en els moviments parabòlics per aconseguir la màxima distància en funció de l’altura del lloc de partida i d’arribada:
- Quan el punt de partida i el d’aterratge estan al mateix nivell, en aquest cas l’angle òptim és l’esmentat de 45º. Per exemple, un corner en un partit de futbol.
- Quan el punt de partida està més baix que el d’aterratge, per norma general l’angle òptim serà més gran. Un exemple clar és en un partit de bàsquet. Per a encertar una cistella des de més lluny, l’angle haurà de ser major A més en aquest esport es dona el cas que com més gran sigui l’angle de sortida major serà el d’entrada a cistella, i per tant més opcions de que la pilota entri neta en el cèrcol i major probabilitat d’encertar.
- Quan el punt de partida estigui més alt que el d’aterratge, el normal és que s’aconsegueixi major distància amb un angle menor. Un exemple serien les disciplines atlètiques de llançament o de salt de longitud. En aquest últim, al fer la batuda el CDG es troba més alt que al aterrar, per això l’angle de batuda òptim oscil·la entre els 18º-22º.

Detall de la trajectòria d’un atleta en un salt de longitud. El CDG en la batuda és més alt que en el moment d’aterratge.
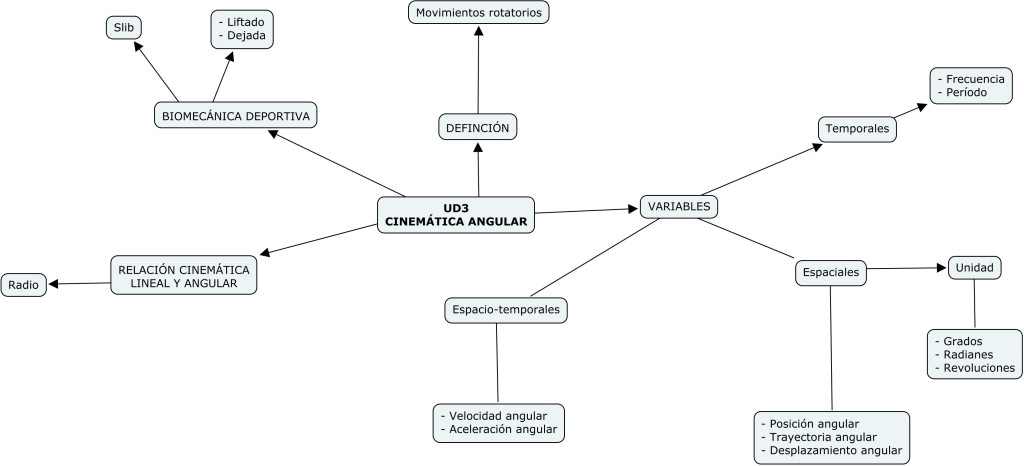
Cinemàtica angular
A diferència de la cinemàtica lineal, a la cinemàtica angular no s’usa com a referència els espais recorreguts sinó els angles aconseguits en realitzar un moviment rotatori sobre un eix.
La majoria dels gestos que es realitzen en l’àmbit esportiu són una combinació de moviments lineals i angulars. Quan un o diversos segments corporals roten al voltant d’una articulació, són moviments angulars; l’eix és l’articulació i els seus graus variaran en funció de l’amplitud articular.
Però no només s’estudiarà la cinemàtica angular a nivell articular, també s’analitzaran on s’executen moviments rotatoris. Per exemple, a la prova atlètica de llançament de martell, on el llançador realitza tres o quatre girs previs al llançament per imprimir acceleració a l’objecte fins que finalment el deixa anar. De la mateixa manera en gimnàstica rítmica, les esportistes llancen les maces, pilotes i cèrcols acompanyats de girs mil·limetrats que encaixen perfectament en el muntatge de la competició.
La cinemàtica angular estudia, quantifica i permet donar respostes a moltes de les qüestions que es plantegen en aquestes disciplines esportives.
Aproximació al concepte de cinemàtica angular
La cinemàtica angular és la segona branca de la cinemàtica i es defineix com a part de la física que estudia les lleis que descriuen els moviments angulars o rotatoris sense analitzar les causes que el provoquen (Rojas, 2008).
Les variables que la defineixen són anàlogues a les comentades en la cinemàtica lineal, però vinculades al moviment angular que es caracteritza per girar al voltant d’un eix de rotació. La conseqüència de que tot el sistema giri alhora sobre aquest eix, és que totes les seves parts realitzen el mateix desplaçament angular en el mateix període de temps.
No passa el mateix amb el desplaçament lineal (Gutiérrez, 1999). Si ens hi fixem, a la figura 1 veurem que les línies contínues vermella i verda corresponen a l’angle vermell a1-a2 que és exactament igual a l’angle verd b1-b2, concretament de 22,5º. En canvi, els desplaçaments lineals d1 i d2, representats per les línies discontínues vermella i verda són diferents.
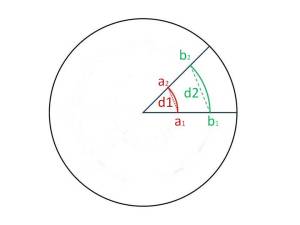
De la mateixa manera que a la cinemàtica lineal, podem dividir les variables de l’angular en temporals, espacials i espai-temporals.
Variables temporals
La freqüència en moviments angulars es defineix com el nombre de girs o rotacions que realitza un cos per unitat de temps. Igualment, el període en moviments angulars també s’obté a partir de l’invers de la freqüència, la qual cosa equival al temps que es tarda en fer una rotació completa.
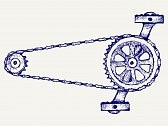
El temps que triga un pedal a fer una volta completa seria el període en el pedaleig.
Variables espacials
Les variables espacials en cinemàtica angular fan referència a la rotació en l’espai que registra un cos, objecte o segment d’aquest, respecte a un punt de referència considerat fix. És a dir, que el cos recorre un angle o bé realitza un desplaçament angular.
Segons la RAE, angle és aquella figura geomètrica formada en una superfície per dues línies que parteixen d’un mateix punt. Un angle es pot configurar per la intersecció de dues línies, dos plans o bé per l’encreuament entre un pla i una línia (Rojas, 2008).
La posició angular d’un cos fa referència a la seva localització respecte a un angle, és a dir, d’una línia respecte a una altra línia o un pla. Igual que en els sistemes de referència de la unitat anterior, quan la línia o pla sobre la qual es detalla el moviment està fixa es parla d’angle absolut. En canvi, quan està en moviment s’anomena angle relatiu (Gutiérrez, 1999).
Un exemple d’angle absolut en l’articulació del colze seria quan el flexionem en posició bípeda sense desplaçament. Per a la mateixa articulació, un angle relatiu seria quan s’estén en un llançament de javelina, ja que l’atleta es troba en moviment després de la carrera i el pas creuat.
La unitat més comuna per mesurar els angles és el grau (º). La RAE defineix grau com cadascuna de les 360 vegades en què es pot dividir una circumferència. Però el Sistema Internacional (SI) també usa com a unitat angular el radian (rad) que equival a 180º / n o el que és el mateix, a 57.295º. El radian ve definit per la longitud del radi d’una circumferència, i equivaldria a l’angle que es forma quan l’arc de la circumferència que abraça té la mateixa longitud que el radi.
Una altra variable de posició és la revolució, que representa un gir complet en un període de temps.
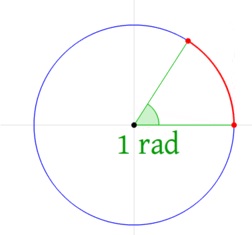
Imatge animada representant el radian.
La distància o trisectora angular és un valor escalar, no vectorial, i representa al conjunt total d’angles recorreguts sense tenir en compte la direcció d’un cos. Per exemple, si un gimnasta realitza un doble mortal, es diu que ha recorregut 720º (360º per 2).
En canvi, el vector desplaçament angular és la variació de la posició angular que experimenta un cos que rota al voltant d’un eix (Rojas, 2008). En definitiva, seria el resultat de restar l’angle final menys l’inicial, d’un cos en rotació. Per tant, el desplaçament angular d’un pedal de bicicleta que realitza una volta completa seria zero perquè el seu punt final i inicial coincideix, en canvi la seva trajectòria seria de 360º.
Variables espai-temporals
Les variables espai-temporals són anàlogues a les de la cinemàtica lineal: velocitat angular i acceleració angular.
La velocitat angular és una variació de gir i per això no es pren com a referència l’espai recorregut sinó l’angle (Aguado, 1993). Es defineix com la variació de la distància angular per unitat de temps (Tipler, 2000). Aquesta variable té caràcter vectorial i es representa per la lletra grega omega (ω).
En el SI la velocitat angular es mesura en radiants per segon (rad/s). A vegades també s’expressa en angles per segons (º/s), en revolucions per minut (rpm) o per segon (rps).
La velocitat angular, en ser un vector, també representa la direcció de gir, per això en algunes ocasions pot tenir valor positiu o negatiu. Seria positiu quan la variació de la distància angular girés en sentit antihorari i negatiu quan ho fes en sentit horari (Tipler, 2000). Però aquesta regla no sempre és presa en compte en l’àmbit de la biomecànica esportiva.
 Una biela dels pedals d’una bicicleta, gira a la mateixa velocitat angular en tots els seus punts, tot i que les zones més properes a l’eix descriguin una velocitat lineal menor. De la mateixa manera, dos atletes que corrin per una pista d’atletisme, un pel carrer 1 i un altre pel carrer 8, si tots dos triguen el mateix temps en córrer un dels revolts, tots dos tindran la mateixa velocitat angular. Però el del carrer 8 anirà a una velocitat lineal major, perquè corre 26,5 m més que el del carrer 1 en el mateix temps.
Una biela dels pedals d’una bicicleta, gira a la mateixa velocitat angular en tots els seus punts, tot i que les zones més properes a l’eix descriguin una velocitat lineal menor. De la mateixa manera, dos atletes que corrin per una pista d’atletisme, un pel carrer 1 i un altre pel carrer 8, si tots dos triguen el mateix temps en córrer un dels revolts, tots dos tindran la mateixa velocitat angular. Però el del carrer 8 anirà a una velocitat lineal major, perquè corre 26,5 m més que el del carrer 1 en el mateix temps.
Quan el moviment no és uniforme i hi ha un increment o disminució de la velocitat angular, apareix la variable acceleració angular. Aquesta es defineix com la variació de la velocitat angular per unitat de temps (Tipler, 2000). També té caràcter vectorial i es representa per la lletra grega alfa (α).
En el SI l’acceleració angular es mesura en radiants per segon al quadrat (rad/s2). A vegades també s’expressa en angles per segons al quadrat (º/s2).
 Quan l’acceleració angular és positiva significa que el cos està en fase d’acceleració, ja que la seva velocitat angular està augmentant. Per contra, valors negatius d’acceleració angular denoten una desacceleració i per tant una disminució de la velocitat angular (Gutiérrez, 1999).
Quan l’acceleració angular és positiva significa que el cos està en fase d’acceleració, ja que la seva velocitat angular està augmentant. Per contra, valors negatius d’acceleració angular denoten una desacceleració i per tant una disminució de la velocitat angular (Gutiérrez, 1999).
Un exemple d’acceleració angular negativa és quan es derrapa amb un skate per aturar. El que es fa és transformar la velocitat lineal en angular i disminuir l’acceleració angular gràcies a la fricció amb el terra.
Relació entre moviment lineal i angular
Quan un cos realitza un moviment angular, l’arc de circumferència que recorre resulta en una successió de punts que no deixa de ser una línia. Si es coneix el radi de la circumferència i els angles recorreguts, pot calcular-se la longitud de l’arc d’aquesta trajectòria segons la següent fórmula, on L és l’arc de circumferència, r el radi i Θ el radi de l’arc:
![]()
Si en comptes de l’angle es coneixen els radians, llavors la fórmula quedaria:
![]()
Al llarg de la unitat s’ha comentat que a una mateixa velocitat angular li pot correspondre diferents velocitats lineals. Com més allunyat de l’eix de gir estigui l’objecte, major velocitat lineal tindrà. Un exemple clar el trobem en comparar el cop de tennis amb el colze flexionat o estès. En el segon cas, el radi de gir sobre l’articulació de l’espatlla serà més gran. Tot i que tota la raqueta va a la mateixa velocitat angular, perquè totes les seves partícules recorren el mateix nombre de graus en el mateix temps, la pilota arribarà a una major velocitat si en el moment del cop el colze està estès.

Rafa Nadal colpejant amb el colze estès.
La relació entre la velocitat angular i lineal és deguda al fet que aquesta última es defineix com un vector tangencial a la corba i perpendicular al radi, per aquesta raó també se li denomina velocitat tangencial. La relació matemàtica entre ambdues velocitats està en funció del radi, segons la següent fórmula:
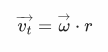
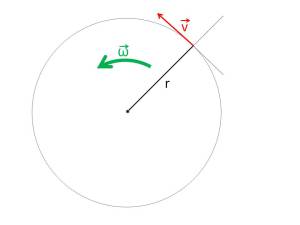
Representació gràfica de la velocitat lineal en un moviment rotatori.
L’acceleració lineal vinculada a un moviment rotatori és com la velocitat lineal, tangencial a la trajectòria, per això també s’anomena acceleració tangencial.
Cinemàtica angular i biomecànica esportiva

Detall del ‘slib’ d’un tir a cistella de bàsquet.
En els llançaments de bàsquet a cistella, sobretot en els tirs lliures, s’imprimeix un gir a la pilota en sentit contrari al seu avanç denominat slib. Abans que la pilota abandoni la mà se li imprimeix un efecte amb una flexió de canell que atorga a la pilota un gir específic. Gràcies a aquesta acció angular la pilota adquireix una trajectòria més bombada el que permet augmentar l’angle d’entrada a cistella (Aguado, 1993). (N. del T. Només he trobat evidència de l’existència d’aquest terme ‘slib’ al llibre d’Aguado, cap resultat més retorna resultats a Google, la qual cosa em resulta estranya, tot i que si que retorna cerques sobre l’efecte Magnus).
A major angle d’entrada, més opcions que la pilota entri neta en el cèrcol i major probabilitat d’encistellar. Només cal imaginar una visió zenital del cèrcol: si ens col·loquem just a dalt del cèrcol la visió que es tindrà d’aquest serà una circumferència perfecta. En canvi si es redueix l’alçada i ens desplacem lateralment, la nostra línia de visió respecte al cèrcol ja no serà perpendicular sinó més diagonal i en lloc de veure un cercle es reduirà a una el·lipse.
Un altre avantatge del slib és que en cas que colpegi la pilota al cèrcol, el rebuig que produeix és menys contundent perquè al girar en sentit contrari al desplaçament queda frenat el rebot. A més, la trajectòria que adquireix és més vertical i per tant té més probabilitats d’entrar a cistella després del rebot.
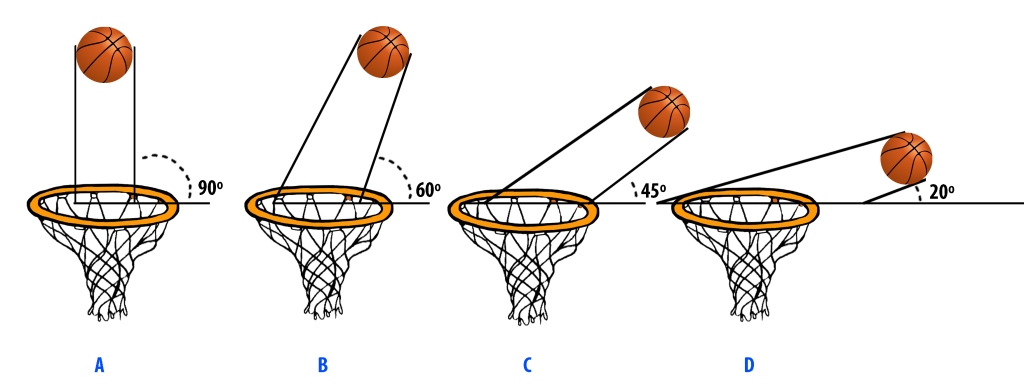
Detall de diferents angles d’entrada a una cistella de bàsquet. El més òptim és el A i el menys el D.
En el tennis també cobra gran importància el gir de la pilota. De fet, el pelatge d’aquestes boles serveix per augmentar l’efecte de gir, gràcies a l’augment del corrent d’aire que arrossega. Per evitar que la pilota surti de la pista quan es colpeja fortament, se li imprimeix un efecte anomenat liftat.

Detalls del pelatge d’una bola de tennis.
L’angle previ o angle d’incidència serà més gran en cas de no aplicar el liftat i la bola botarà més a prop de la xarxa. Per contra, l’angle posterior al bot o angle de reflexió serà menor que de no haver tingut gir, i per tant dificulta la resposta del contrari. Una altra avantatja és l’augment de la velocitat de la bola després del rebot, a causa del fregament amb la pista durant l’impacte, part de la velocitat de gir es suma a la velocitat horitzontal (Aguado, 1993).
Per contra, un altre gest tècnic del tennis és el cop tallat, que produeix un efecte similar al slib de bàsquet. El cop s’efectua de dalt a baix i gairebé sense impuls de darrere cap a endavant. La pilota adquireix un gir en sentit contrari al del seu avanç. Com a conseqüència la trajectòria és més parabòlica i l’angle de reflexió és més gran que en cops sense efecte i molt més gran que en el liftat. D’aquesta manera la pilota redueix la component horitzontal de la velocitat per la fricció amb el terra en el rebot, produint la típica deixada d’aquesta acció.

En el liftat (esquerra) l’angle d’incidència (α) és major que el de reflexió (β). En la deixada (dreta) succeeix al revés.
En resum
La biomecànica requereix d’un sistema de referència per estandarditzar l’observació del moviment dels cossos, i pot ser absolut o relatiu.
En aquest sentit la cinemàtica lineal estudia aquells moviments de tipus lineal i parabòlic.
Per estudiar el moviment es registren variables temporals (temps, freqüència i període), espacials (posició, trajectòria i desplaçament) i variables espai-temporals (velocitat i acceleració).
En funció de com interactuïn aquestes magnituds, els moviments poden ser:
- A velocitat constant
- Accelerats: uniformement o variablement accelerats.
- Desaccelerats: uniformement o variablement desaccelerats.
Una de les trajectòries més estudiades en biomecànica és la dels moviments parabòlics. Aquest moviment està condicionat per dos tipus d’agents: externs al sistema (força de la gravetat i la resistència de l’aire) i intrínsecs al sistema (velocitat inicial de sortida i l’angle de projecció respecte a l’horitzontal).
En canvi, quan el punt de partida està més baix que el d’aterratge, haurà de ser major de 45º. Per contra, quan el punt de partida està més alt que el punt d’aterratge, ha de ser menor de 45º.
Un altre aspecte important pel que fa als graus de sortida és el dels angles complementaris, aquells que sumin 90º arribaran a la mateixa longitud.
D’altra banda, la cinemàtica angular és la segona branca de la cinemàtica i es defineix com la part de la física que estudia les lleis que descriuen els moviments angulars o rotatoris sense analitzar les causes que el provoquen.
En els moviments angulars tot el sistema gira alhora sobre aquest eix, i per tant totes les seves parts realitzen el mateix desplaçament angular en el mateix període de temps. Però no passa el mateix amb el desplaçament lineal.
Les variables pròpies de la cinemàtica angular s’agrupen en temporals (freqüència i període), espacials (posició angular, distància o trajectòria angular i desplaçament angular), i finalment les espai-temporals (velocitat angular i acceleració angular).
La unitat més comuna per mesurar els angles és el grau (º) però el sistema internacional (SI) fa servir com a unitat angular el radiant (rad) que equival 180º/p, o el que és el mateix 57,3º.
Entre el moviment lineal i angular ha una estreta relació en funció de la longitud del radi de gir. A partir d’aquesta dada es pot calcular l’analogia de les variables lineals a partir de les angulars i viceversa.
En la biomecànica esportiva existeixen nombrosos estudis on s’aplica la cinemàtica angular. Un dels exemples és en el slib que se li imprimeix a la pilota de bàsquet. També en l’efecte liftat o de deixada de les pilotes de tennis té una gran implicació la cinemàtica angular.