En l’entrada anterior de les unitats 2 i 3 varem veure els conceptes claus sobre cinemàtica lineal i angular. Avui li toca el torn a les unitats 4 i 5 que tracten sobre cinètica: dinàmica i estàtica respectivament. Recordem l’esquema general vist a la primera unitat introductòria a la biomecànica esportiva, segons Xavier Aguado (1993):

Nota
Com ja sabeu, totes les entrades de la secció apunts del Grau en Nutrició Humana i Dietètica i Ciencies de l’Activitat Física i l’Esport estan extretes del material proporcionat per la Universitat Isabel I de Castilla. A més, en aquesta assignatura en particular, hi ha una bona feina de redacció per part de l’equip docent que la coordina. Els corresponents crèdits, doncs, a la universitat i a l’equip. La meva missió aquí només és traduir-los i aportar alguns enllaços extra com a material addicional.
Cinètica Dinàmica
La Dinàmica és la branca de la Física mecànica que estudia les causes que produeixen el moviment dels cossos. El seu objectiu és descriure els factors capaços d’originar aquests canvis, quantificar-los i establir fórmules matemàtiques que els representin. La dinàmica té dues vessants, la cinètica i l’estàtica.
La causa mecànica que origina el moviment o el modifica s’anomena força. Per tant, la dinàmica serà l’estudi de les forces que actuen en un cos per produir el moviment d’un cos o alterar-lo.
Hi ha diversos instruments que mesuren la força dels cossos com la plataforma de força, la plataforma de pressions, o potenciòmetres entre d’altres. Tots ells tenen la particularitat d’aplicar els principis físics de la dinàmica a la biomecànica esportiva.
Al llarg d’aquesta unitat es mostrarà com la dinàmica serveix per explicar mecànicament tècniques esportives d’esports com el judo, el llançament de martell o la gimnàstica esportiva.
Aproximació al concepte de força
Definició de força i pes
En mecànica el concepte de força està associat a la interacció entre un objecte amb el seu entorn i es configura com aquell agent que canvia o tendeix a canviar la situació de repòs o moviment d’aquest objecte. Segons la Real Acadèmia de la Llengua, es defineix força com la causa capaç de modificar l’estat de repòs o de moviment d’un cos o de deformar.
Per exemple, una pilota de futbol estarà en repòs en el punt de penal fins que un jugador la copegi i apliqui una força en ella, que per una banda la deformarà en el moment de l’impacte i de l’altra la dotarà de moviment fins que el porter apliqui una altra força per aturar-la o rebutjar-la. I en realitat és una descripció molt simple perquè s’han obviat altres forces que interaccionen per modificar l’estat de moviment de la pilota en l’aire com són la força de la gravetat o força de resistència amb l’aire, entre d’altres.
La força és una magnitud que té caràcter vectorial, per tant té direcció i sentit. La seva unitat és el newton i es representa per una N majúscula.
En relació amb la força pròpia dels cossos, hi ha dos magnituds que han de ser ben diferenciades: la massa i el pes.

Tot i que la massa de la barca és la mateixa, moure-la en la sorra ens exigirà més esforç que quan flota a l’aigua.
La massa d’un cos és una magnitud escalar que representa la quantitat de matèria que té un cos. Es representa per la lletra m minúscula i la seva unitat en el SI és el quilogram (kg). La massa és una característica intrínseca als cossos i mesura la resistència d’aquests a l’acceleració, per això caldrà aplicar més força a una pilota medicinal de 5 kg que a una pilota de bàsquet d’uns 0.6 kg, tot i que tots dos tenen un volum similar. La massa és sempre la mateixa per a un cos independentment d’on estigui: si la pilota de bàsquet està en l’aigua donarà la sensació que “pesa” menys que en l’aire, però la seva massa serà la mateixa encara que suri.
En canvi, el pes és una magnitud vectorial i representa la força que exerceix un cos en relació amb la gravetat. És en si, la força amb què la massa d’un cos és atreta cap al centre de la Terra (Alegre, 2008). El pes en ser una força es mesura també en Newton i és directament proporcional a la massa del cos i a l’acceleració de la gravetat (que en el cas de la Terra es pren com a estàndard 9.8 m/s2.
Es representa per la següent fórmula:
Classificació de la força
Segons Brancazio (1984) l’estudi de la força en l’àmbit esportiu es pot organitzar segons la seva classificació en dos grups: forces de contacte i forces sense contacte.
Les forces de contacte són aquelles que són exercides per un cos directament sobre un altre. Per exemple quan es colpeja amb una raqueta una pilota de tennis. Respecte a les forces sense contacte estarien la força de la gravetat o la força centrífuga en un revolt.
Al seu torn, Alegre (2008) agrupa els tipus de força en les següents categories:
- Forces de reacció: si colpegem una enclusa amb un martell, el martell rebotarà a causa de la força de reacció que l’enclusa exerceix sobre ell.
- Fora ascensional: és la força que experimenta un cos quan està submergit en un fluid, ja sigui líquid o gasós. Gràcies a aquesta força suren els vaixells a l’aigua o volen els globus aerostàtics. En el cas de l’aigua es denomina força de flotació.
- Força de fregament: s’originen en interaccionar dos o més superfícies entre si. Quan major força de fregament s’origini entre la sola de la sabata i el terra, menor serà la probabilitat de relliscar.
- Força de resistència: és la força que dificulta l’avanç d’un sòlid en un fluid o el pas d’un fluid pel cos. Com més aerodinàmic sigui un cotxe, menor serà la resistència que li ofereix l’aire.
- Força de sustentació: s’originen en cossos que es desplacen per fluids (gasosos o líquids) a causa dels perfils amb els que s’enfronten al fluid. Gràcies a aquesta força un parapent pot romandre hores planejant o un disc volador es queda com levitant en l’aire.
- Força centrífuga: es dóna en moviments rotatoris, i és la força cap a fora que experimenta els cossos en aquests moviments.
- Força centrípeta: també es dóna en moviments angulars, però en aquest cas és la força que experimenten els cossos cap a dins.
Les lleis de Newton

Isaac Newton (1642-1727)
L’any 1686 Isaac Newton, físic, filòsof i matemàtic anglès, publicà el seu llibre Philosophiae Naturalis Principia Matematica. Aquesta obra configura la base de la mecànica moderna i en ella l’autor exposa les seves tres lleis del moviment i la seva llei de gravitació universal.
Primera llei de Newton
Diu que tot cos romandrà en estat de repòs o en moviment rectilini uniforme mentre no hi hagi forces externes que actuen sobre ell (Tipler, 2000).
Es denomina també llei de la inèrcia, que en mecànica es defineix com la resistència que ofereix un cos a modificar el seu estat de repòs o moviment. És proporcional a la seva quantitat de matèria, per això, com més gran sigui la massa d’un cos, major serà la resistència a modificar el seu estat. Per moure un pes de 5 kg lògicament haurem de fer menys força que per a una de 100 kg.
Aquesta primera llei no diferencia si un cos està en repòs o en moviment rectilini uniforme, perquè en certa manera quan s’està en repòs la seva velocitat és constant i amb un valor de 0 m/s.
Segona llei de Newton
Quan una força actua sobre un cos, aquest experimenta una acceleració proporcional a aquesta força que tindrà la mateixa direcció i sentit (Gutiérrez, 1999).
Si la primera llei de Newton afirma que per tal que un cos modifiqui el seu estat de repòs o moviment cal que s’apliqui una força sobre ell, la segona llei de Newton fa referència a la forma de quantificar aquesta força. Per a això es tenen en consideració dos aspectes:
- Que la força i la seva consegüent acceleració són proporcionals
- Que la constant de proporcionalitat que es pren en consideració és la massa del cos.
Per això, la segona llei de Newton es pot expressar amb la següent fórmula:

Aquesta fórmula, a més de quantificar la força, permet també definir la seva unitat, de manera que un Newton (N) serà la força que cal exercir sobre un cos d’un quilogram de massa perquè adquireixi una acceleració d’1 m/s2.
Un altre aspecte a considerar en aquesta fórmula rau en que en ser la força una magnitud vectorial, l’acceleració resultant tindrà la mateixa direcció i sentit, com bé diu la llei.
Tercera llei de Newton
Quan un cos exerceix una força d’acció sobre un altre, aquest reacciona amb una força del mateix mòdul i direcció però de sentit contrari (Alegre, 2008).
Per exemple, quan se salta sobre un llit elàstic s’aprecia que en empènyer amb el nostre cos cap avall, la superfície del llit es deforma, aquesta seria la força d’acció. Després aquesta impulsa el subjecte cap amunt, el que seria la força de reacció. De la mateixa manera, quan una pilota colpeja a un jugador (força d’acció) torna a sortir rebotada (força de reacció).

Tot i que la força de reacció és proporcional a la d’acció, la seva intensitat i direcció variaran en funció de les característiques de les superfícies de contacte. Si una pilota colpeja en una superfície en forma de vèrtex aquest podrà sortir en una altra direcció ben diferent.
De la mateixa manera, si en lloc de saltar en un llit elàstic es salta sobre la sorra de la platja, una part de la força d’acció serà absorbida reduint la força de reacció i per tant l’alçada del salt.
Durant la carrera, l’impacte de la gambada a terra produeix una força de reacció que es projecta en dues vessants: en impuls, per aixecar el peu que continuï amb la carrera i en vibracion,s que han de ser absorbides per l’organisme. Córrer per superfícies molt dures com l’asfalt sotmet a les articulacions, musculatura i tendons a altes freqüències de vibracions que poden desencadenar sobrecàrregues i lesions. Això es deu a que aquest tipus de superfícies no es deformen i amb prou feines absorbeixen la força d’acció o impacte.
Les sabatilles d’esports amb sistemes especials d’amortiment ajuden a minimitzar aquestes vibracions. Per contra, superfícies excessivament toves, com la sorra de la platja, són també contraproduents perquè al ser molt flexibles i deformables redueixen la força de reacció al mínim. Aquest fet sotmet l’organisme a situacions d’estrès i sobrecàrrega precisament per la inestabilitat de la superfície i l’absència de vibracions. Superfícies com la gespa o la terra són les més idònies per a la carrera: ni excessivament toves, ni excessivament dures.

Superfícies com la gespa o la terra són les més idònies per a la carrera: ni excessivament toves, ni excessivament dures.
Impuls mecànic i quantitat de moviment
De la segona llei de Newton es poden deduir dos conceptes cinètics: impuls mecànic i quantitat de moviment.
L’impuls mecànic seria la variació de la força exercida sobre un cos en funció del temps que està actuant (Aguado, 1993). La fórmula que defineix aquest concepte prové de la combinació de les fórmules de la força i l’acceleració.

L’impuls mecànic és una magnitud vectorial que tindrà la mateixa direcció i sentit que la força que s’aplica i la seva unitat és el newton per segon, N/s.
En el cas del llançament de javelina, una petita força aplicada durant molt de temps podrà implicar el mateix impuls mecànic que una força gran aplicada durant un període curt de temps. L’opció més eficient estarà en funció d’una força i temps que permeti a la javelina adquirir l’acceleració òptima per a assolir la màxima distància.
Però l’impuls mecànic també té especial rellevància en moviments desaccelerats. Per exemple quan un jugador de bàsquet realitza una esmaixada i amorteix el seu retorn a terra.
La quantitat de moviment o moment és una magnitud vectorial que es defineix com el producte de la massa d’un cos per la variació de la velocitat. Tindrà la mateixa direcció i sentit que la velocitat i la seva fórmula deriva de les mateixes que l’impuls mecànic: la de la força i de l’acceleració (Gutiérrez, 1999).
Es representa per una p minúscula i la seva unitat és el kg · m/s, quedant:
![]()
Una pilota de futbol en el punt de penal no tindrà quantitat de moviment perquè està en repòs i la seva velocitat és zero. Fins que no sigui colpejada no adquirirà velocitat, i per tant quantitat de moviment. Per aconseguir grans quantitats de moviment s’han de desplaçar grans masses a velocitats moderades, per exemple un jugador de rugbi de 100 kg a 3 m/s. O bé masses moderades a altes velocitats, per exemple un nen de 20 kg a 15 m/s. En ambdós casos la quantitat de moviment serà la mateixa 300 kg · m/s.
Tant la fórmula anterior com els exemples corresponen al que s’anomena moment lineal, ja que es refereixen a velocitats lineals. Quan s’estudien moviments rotatoris es parla de moment angular i en lloc de velocitats lineals pot usar-se velocitats angulars. És també una magnitud vectorial amb la mateixa direcció i sentit que la velocitat angular i es representa per la lletra L majúscula.
La seva unitat és kg · m/s2 i el seu càlcul es realitza mitjançant la següent fórmula:
![]()
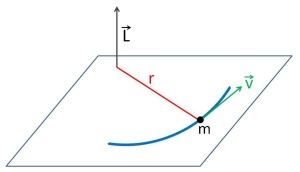
Representació gràfica del moment angular.
Conservació de la quantitat de moviment
La primera llei de Newton descriu que un cos que està quiet o en moviment uniforme romandrà així fins que alguna força externa el modifiqui. Quan dos o més cossos xoquen entre si es produeix un intercanvi en la quantitat de moviment entre ells, de manera que la quantitat de moviment inicial ha de ser igual a la quantitat de moviment després de la col·lisió. Aquesta afirmació es coneix com Principi de la conservació del moviment.
En l’exemple anterior del penal de futbol, el moment del jugador abans de llançament serà igual al de la pilota després del cop, més el del jugador, perquè aquest no queda totalment quiet sinó que continua amb la inèrcia del moviment.
En una pista de patinatge si considerem que no hi ha fregament amb la superfície, un patinador de 50 kg que queda frenat en xocar contra un altre patinador de 100 kg que està aturat en la seva mateixa direcció i sentit, sortirà desplaçat a una velocitat que serà la meitat que la del primer patinador, perquè el seu pes és el doble. La velocitat amb la qual surt desplaçat el segon estarà en funció de la velocitat i massa del primer patinador (a major velocitat i massa major velocitat del segon) i de la massa del segon (a menor massa major velocitat).

En un pèndol múltiple es compleix el Principi de la conservació del moviment, que va passant d’una bola a una altra fins que arriba al final, sortint acomiadada a la mateixa velocitat i altura que la del principi.
En la conservació del moment hi ha una sèrie d’axiomes que sempre es compleixen (Alegre, 2008):
- Com més gran sigui l’impuls que rep un objecte en repòs, major serà la velocitat final.
- Davant mateixos impuls, com menor sigui la massa del cos que el rep, major serà la velocitat final.
- Com més gran sigui el temps que s’aplica a una mateixa força a un mateix cos, major serà la velocitat final.
Els exemples anteriors són representatius de la conservació del moment lineal, però els moviments rotatoris també compleixen el principi de conservació del moment, però en aquest cas angular. La diferència rau en que entra una nova variable en joc, el radi. Un exemple evident de la conservació del moment angular s’aprecia en els girs que sobre si mateix realitzen els patinadors artístics. Com més agrupat estigui el patinador, menor serà el seu radi i major serà la seva velocitat angular per mantenir la quantitat de moviment.
En els mortals de gimnàstica esportiva passa el mateix, quan es realitza un planxa que no aconsegueix la suficient altura o velocitat de gir, el gimnasta s’agrupa per disminuir la seva ràdio, augmentar la seva velocitat angular i aconseguir així aterrar amb els peus a terra.
Però la conservació del moment també es dóna entre moviments lineals i angulars. Quan un cotxe a gran velocitat colpeja a un altre i comença a rodar, el que ha passat és que el moment lineal s’ha transformat en moment angular. Com més baix sigui el radi de gir més gran serà la velocitat angular. El mateix passa quan es fa un placatge en rugbi, el jugador que placa tendeix a fer rodar l’adversari per evitar un cop sec que té més possibilitats de lesionar.
A la figura de sota s’aprecia una projecció de judo anomenada Tomoe nage, en la qual l’uke (defensor) empeny linealment al tori (qui executa la projecció), aquest últim es deixa caure en aquesta direcció per a projectar cap enrere a l’uke fent-lo girar sobre el seu peu dret.
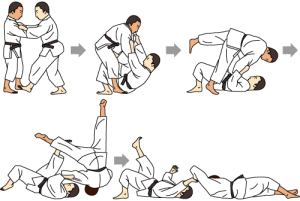
Tomoe nage, tècnica de judo. Imatge agafada de Judo Channel.
Cinètica Estàtica
Com ja varem introduir a la unitat didàctica 1, la Dinàmica és la part de la física dedicada a l’estudi de les causes que provoquen o modifiquen el moviment dels cossos (Aguado, 1993). Dins d’aquest camp de la física, l’estàtica estudia les forces encarregades de mantenir els cossos en equilibri (Aguado et al. 1997).
A continuació estudiarem l’equilibri i l’estabilitat aplicats a diverses situacions físic-esportives. S’ampliaran els coneixements vists fins ara sobre el centre de gravetat i s’aprofundirà en altres conceptes paral·lels.
Aproximació al concepte d’equilibri i classificació
Concepte d’equilibri
En la següent imatge, la palanca (caldria veure els apunts de l’assignatura de cinesiologia sobre tipus de palanques) està en equilibri perquè totes les forces externs que interaccionen en el sistema s’anul·len, donant com a resultat una eficiència mecànica de zero.
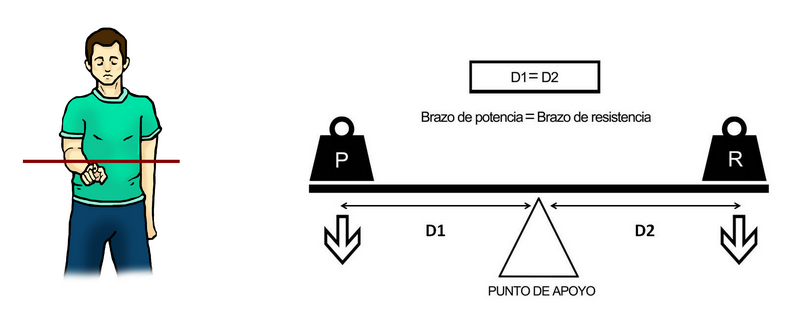
Persona sostenint un llistó de fusta en equilibri i representació de la palanca de primer grau o gènere que conforma.
La RAE defineix equilibri en la seva primera accepció com estat d’un cos quan forces oposades que obren en ell es compensen destruint-se mútuament. Això no vol dir que no hi hagi forces o moments de forces actuant, sinó que els vectors s’anul·len entre si (Aguado, 1993).

Els funambulistes estan en equilibri sobre la corda fluixa però no estan totalment quiets.
Però aquesta és la definició des del punt de vista de la física mecànica. En biomecànica, l’equilibri es vincula al manteniment d’una posició al llarg del temps sense perdre-la. Això no vol dir que el cos no tingui cap moviment, més aviat tot el contrari, l’equilibri és una re-equilibració constant. Quan un subjecte roman dempeus molt de temps no està totalment quiet sinó que realitza petits balanceigs entorn a una mateixa posició d’equilibri.
Variables associades a l’equilibri
A partir d’aquesta interpretació sorgeix el concepte d’estabilitat. López (2008) el defineix com la capacitat que tenen els cossos per mantenir l’equilibri i evitar ser desequilibrats. L’estabilitat s’associa a la dificultat que presenta un cos per perdre el seu equilibri en aplicar forces desequilibradores (Aguado, 1993).
La segona accepció que la Reial Acadèmia de la Llengua atribueix al concepte equilibri va en aquest sentit: situació d’un cos que, tot i tenir poca base de sustentació, es manté sense caure. Aquesta definició introdueix una nova variable determinant de l’equilibri: la base de sustentació (BDS).
Aguado (1993) defineix la BDS com l’àrea d’un polígon format per les arestes que uneixen els punts extrems amb el qual es recolza o sosté un cos. Aquestes arestes o línies que uneixen els punts de suport reben el nom de arestes de caigudes. Com més gran és la BDS més estabilitat té el sistema.
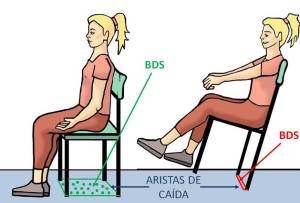
Detall de la BDS en dos sistemes similars. La BDS de l’esquerra és més gran que la del sistema de la dreta i per tant més estable.
El centre de gravetat (en endavant CDG) és una altra variable associada a l’equilibri, però donada la seva rellevància, en parlarem amb més detall en breu.
L’última variable a tractar és l’angle de caiguda, que es defineix com l’angle que forma la línia que uneix el CDG amb una aresta de caiguda, i aquesta mateixa aresta amb la vertical.
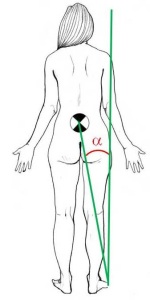
Angle de caiguda.
Classificació de l’equilibri
Els equilibris es classifiquen en funció de l’estabilitat que tenen els cossos i la complexitat que presenten per a ser desequilibrats. Es classifiquen en: equilibri estable, equilibri inestable, equilibri indiferent i equilibri hiperestable (Aguado, 1993).
- L’equilibri estable és molt difícil de desequilibrar, per la qual cosa precisa d’una gran força externa o pertorbadora que modifiqui el seu estat. A la figura 4, el sistema de l’esquerra representa un equilibri estable.
- L’equilibri inestable és aquell que només precisa d’una petita força pertorbadora per alterar la seva estabilitat. A la figura 4, el sistema de la dreta és un exemple evident d’un equilibri inestable.
- L’equilibri indiferent consisteix en un sistema en què en aplicar una força, el cos es desplaça però no es desequilibra, conservant la mida de la seva BDS i mantenint l’altura del CDG. Un exemple clar és el d’una bola, es desplaça fàcilment però sempre té la mateixa BDS i la posició del CDG.

Finalment el equilibri hiperestable està representat per aquells cossos o sistemes que sempre mantenen l’equilibri malgrat rebre grans forces pertorbadores. Es dóna quan el CDG està en contacte amb la BDS, per exemple els ninots saltamartins o “tossuts” (tentetieso en castellà o weeble en anglès). Aquests ninots tenen molt això en la seva base dotant de gran estabilitat.
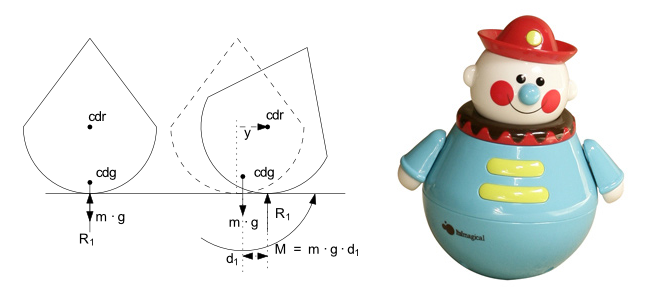
Ninot saltamartí, tossut o “tentetieso”, imatge adaptada del blog Haciéndome el Sueco.
També es dóna quan el CDG està per sota de la BDS. Per exemple un gimnasta que està agafat de la barra fixa, la BDS la configura les seves mans agafades a la barra, i el CDG està per sota.
Sabies que…
A mesura que l’home creix fa servir posicions menys estables i que precisen d’un control neuromuscular més precís. Es passa del gateig, a deambular amb els genolls flexionats i peus separats (baixant el CDG i augmentant la BDS), fins arribar al deambular bípede. Quan s’envelleix i el control neuromuscular és menys eficient, es retorna a posicions més estables: separant els peus i fent servir bastons.
Centre de gravetat
El centre de gravetat és el lloc en què es concentraria tot el pes del cos si fos comprimit des de totes direccions (López, 2008). Seria el punt on conflueix la força resultant del pes de tots els segments d’un cos (Tipler, 2000). Per això el CDG és considerat un punt d’equilibri, ja que en ell s’anul·larien totes les forces derivades del pes del cos.
D’aquesta forma, hi ha la mateixa quantitat de pes repartida entre el CDG i la part superior del cos, que entre aquest punt i la part inferior. Igualment passa entre el pes de la zona anterior al CDG i el pes a la zona posterior. Per últim, també coincidiria la quantitat de pes que hi ha entre el CDG i la zona esquerra pel que fa a la dreta (López, 2008).
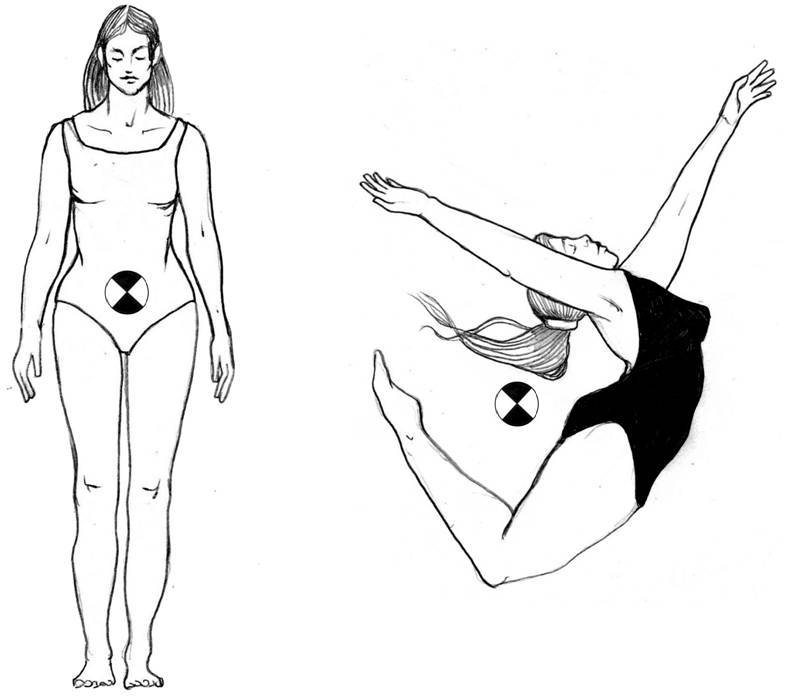
Detall del centre de gravetat en diferents posicions.
Els cossos normalment es poden dividir en segments, de manera que cada un té el seu particular CDG. La sumatòria de tots aquests punts convergiria en el CDG del cos. El CDG no té per què estar en el centre físic del cos, és més, pot ser que es trobi fins i tot fora del cos.

Detall del centre de gravetat en el salt d’altura estil fosbury.
A mesura que es mobilitza un segment corporal en l’espai, part del pes es desplaça en aquesta direcció i per tant varia la posició del CDG. En l’àmbit esportiu constantment s’ajusta la posició del CDG.
Per exemple, els saltadors d’altura a l’executar l’estil fosbury, deixen passar el seu CDG per sota del llistó mentre la resta del cos passa per sobre, tal com es mostra a la figura inferior.
De manera similar, en els exercicis de barra d’equilibri de gimnàstica esportiva femenina, les gimnastes procuren que el CDG sempre estigui en la mateixa línia vertical que la barra i evitar així desequilibris laterals.
La línia vertical imaginària que uneix el CDG amb el terra es denomina línia de gravetat (LDG). Si la projecció de la LDG s’ubica dins de la BDS el cos estarà estable, en canvi si es projecta fos el cos tendirà a caure.
Un altre terme vinculat al CDG és el centre de masses (CDM). Són conceptes similars que solen donar lloc a confusió i en ocasions, són considerats erròniament sinònims. El CDM és el punt mig on es concentraria tota
la massa d’un cos, mentre que el CDG fa referència al pes d’un cos. Igual que ocorre amb la massa i el pes d’un cos, la deferència rau en l’acceleració gravitatòria.
El CDM d’un cos seria el mateix a la Terra que a la Lluna, però el CDG podria ser diferent. En condicions normals, com l’acceleració gravitatòria és constant, el CDG i el CDM coincidiran en el mateix punt, d’aquí que es confongui com un mateix concepte.
Variacions del CDG
Com s’ha esmentat en el punt anterior, a mesura que es mobilitzen les extremitats el CDG també es desplaça de lloc. Quan un pare agafa un nen en braços, es crea un nou sistema, el CDG del qual estarà en una posició intermèdia però més proper al pare perquè el seu pes és més gran. De la mateixa manera, quan s’entrena amb peses, el CDG del subjecte tendeix a desplaçar-se cap el CDG de la manuella (“mancuerna”), tal com es representa en la següent imatge:
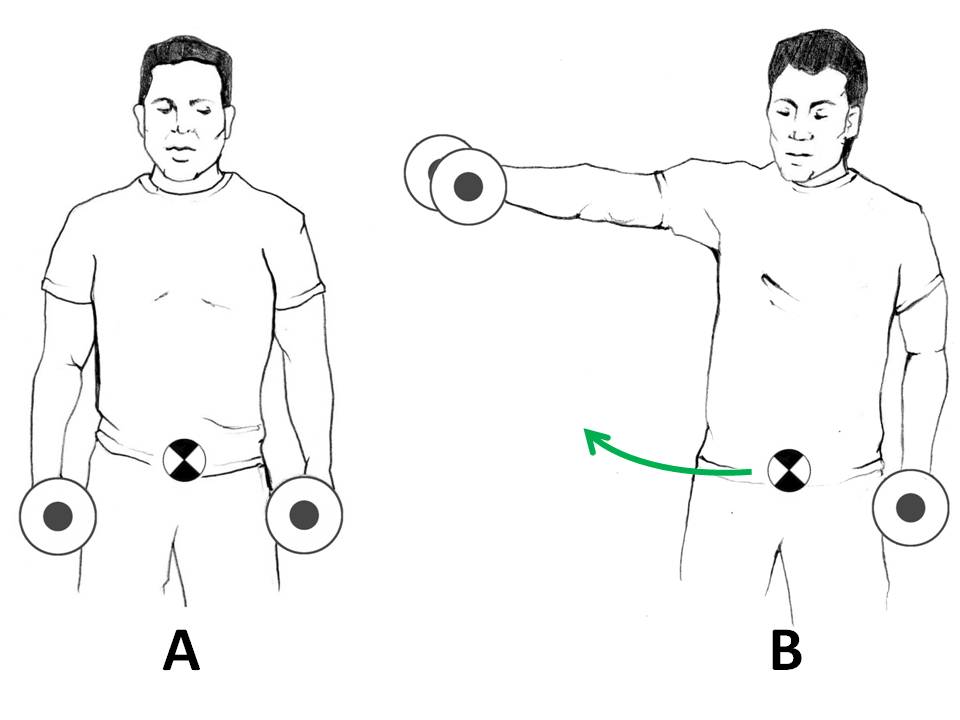
Detall del desplaçament del CDG en un exercici de peses.
En la posició A de la imatge anterior el CDG s’ha desplaçat lleugerament cap avall a causa del pes de les manuelles, però la seva posició continua sent estable. A la imatge B, el CDG es desplaça cap a la dreta i lleugerament cap amunt, pel que la seva posició quedarà lleugerament desestabilitzada cap a aquest costat.
Per evitar aquest tipus de desequilibris el subjecte podria fer l’exercici amb dos braços alhora de manera que la LDG romangués al centre de la BDS. D’aquesta manera també s’evitarien sobrecàrregues innecessàries de la musculatura paravertebral.
També podem observar que a la imatge B el subjecte ha desplaçat lleugerament el seu tronc cap al costat contrari al braç aixecat, d’aquesta manera ha compensat lleugerament el desplaçament cap al seu costat esquerre.
El CDG també pot variar en funció del desenvolupament muscular dels individus. Si augmenta la hipertròfia muscular del tren superior, el CDG tendirà a pujar i viceversa. En aquest sentit, Zatsiorsky (2002) va estudiar la posició del CDG en relació a l’altura del subjecte. Va concloure que els patinadors de velocitat, amb un gran desenvolupament de la musculatura del tren inferior, tenien el CDG un 1,1% més baix que els remers, el tren superior dels quals estava musculat.
Al llarg de l’edat també varia el CDG. La proporció del pes del cap en els nens és més gran que en adults, i per contra la del tren inferior és menor. En definitiva, els nens tenen el CDG més a prop del cap que els adults (Palmer, 1944).
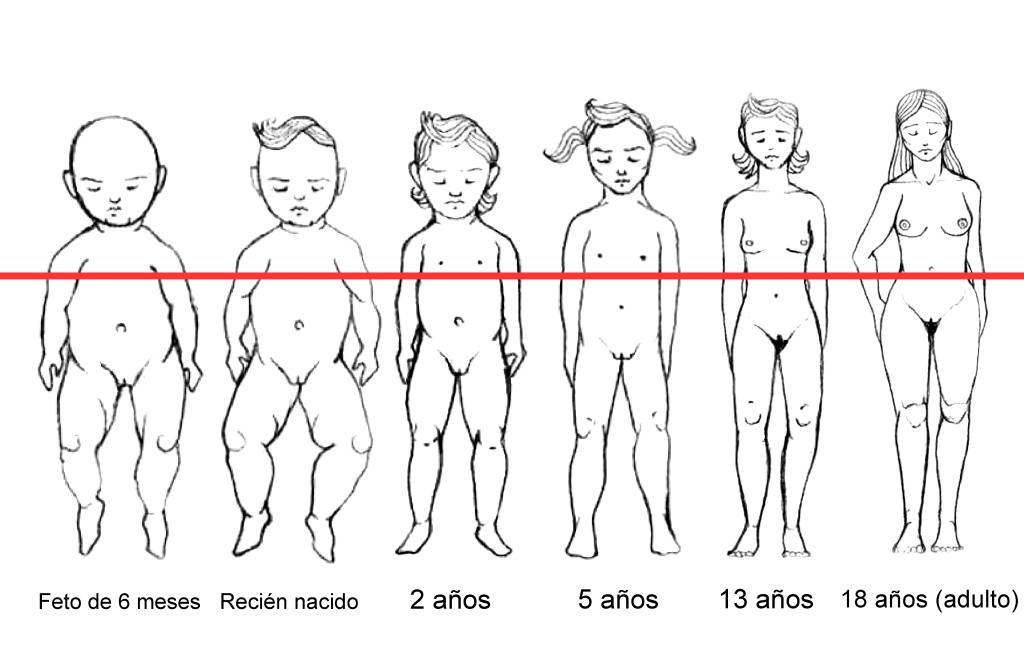
Detall de la variació del CDG al llarg de l’edat.
De la mateixa manera, l’alçada mitjana del CDG varia en funció del sexe. Els homes solen tenir-lo a un 56.18% de la seva talla mentre que la dona al 55.44% (Aguado, 1993).
Mètodes per a calcular el CDG
Hi ha dos tipus de mètodes per calcular el CDG: mètodes directes i mètodes indirectes (Aguado et al, 1997). Els mètodes directes són aquells que es realitzen sobre el cos del qual es desitja conèixer el seu CDG. El seu gran avantatge és que reporta una gran precisió, però té com a inconvenient que només es pot conèixer en posicions estàtiques i per tant mai en competició (López, 2008).
Els mètodes indirectes no necessiten el cos real per al seu càlcul, sinó que es realitza sobre una fotografia. El gran avantatge és que es pot fer sobre una posició adoptada i fotografiada durant la competició, però en contra té l’inconvenient que necessita processos més laboriosos i amb menys precisió que els directes (Aguado et al, 1997).
En aquest apartat s’exposaran dos mètodes directes.
Practica
A la pràctica de laboratori d’aquesta unitat s’explica el procés per a obtenir el CDG amb el mètode indirecte, a partir d’una fotografia superposada en una quadrícula, i calculant els diferents segments corporals. Si li voleu donar una ullada, us comparteixo l’enunciat 😉
Mètode directe de la plomada
Aquest mètode necessita que l’objecte sigui suspès des de qualsevol dels seus punts de manera que pugui girar lliurement sota l’acció de la força de gravetat. Una vegada que deixa d’oscil·lar, el CDG serà a la LDG i gràcies a la plomada es marcarà aquesta línia en el cos. Posteriorment es repeteix aquest procés en un o dos punts més, depenent de la forma de l’objecte (Tipler, 2000).
El CDG es trobarà en la intersecció de tots ells, tal com es mostra a la figura següent:
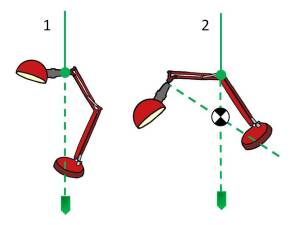
Càlcul del CDG mitjançant el mètode de la plomada. Es penja l’objecte des de diverses parts. Les línies verticals de gravetat sempre es creuen en el CDG.
Mètode directe de Reynolds i Lovett
Aquest mètode va ser proposat per Reynolds i Lovett l’any 1909 i s’usa per conèixer el pla transversal que talla el CDG d’una persona.
Es basa en una proposta que va fer Giovanni Alfonso Borelli al segle XVII. Consistia en una mena de balancí on un subjecte es col·loca damunt d’una taula sobre un fulcre (López, 2008). Quan el sistema s’equilibra implica que el CDG es situaria en la vertical del fulcre.
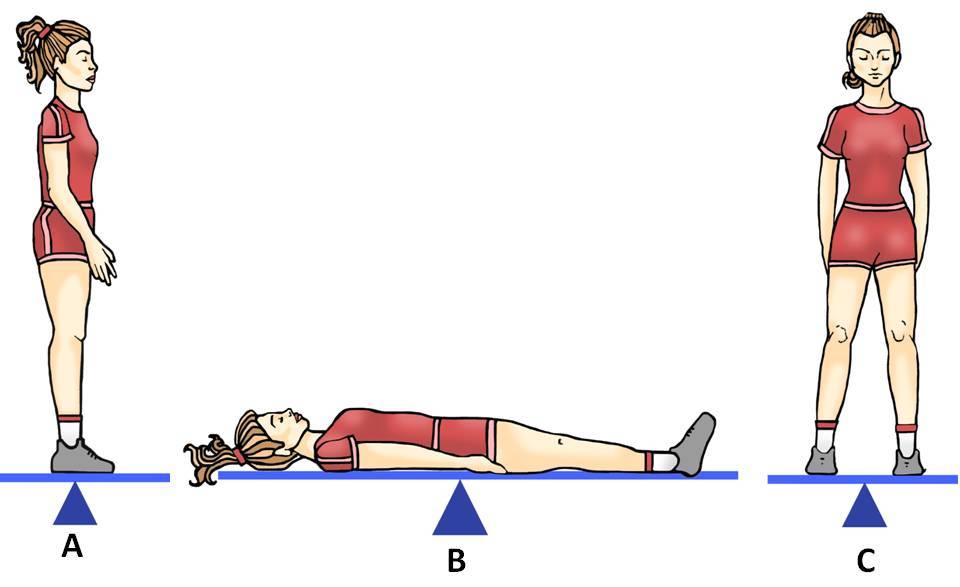
Detall de l’equilibri de Borelli sobre el pla sagital (A), transversal (B) i frontal (C).
Per a això es precisa entre altres objectes d’una bàscula i un tauló que sigui més llarg que l’altura del subjecte a estudiar. En primer lloc s’ha de conèixer l’alçada i el pes del subjecte.
Per realitzar el càlcul s’ha de col·locar el tauler tombat amb un extrem a la bàscula i l’altre sobre uns suports de manera que quedi totalment horitzontal. S’anota el pes de la taula en aquesta posició (pes parcial del tauler).
La persona es tomba sobre el tauler amb les mans enganxades al llarg del cos amb el cap en direcció a la bàscula. Els peus han d’estar en la vertical del centre dels suports de l’altre extrem, tal com es mostra a la figura de baix. En aquesta posició s’anota el pes que marca la persona amb la taula (pes parcial de la persona-taula).
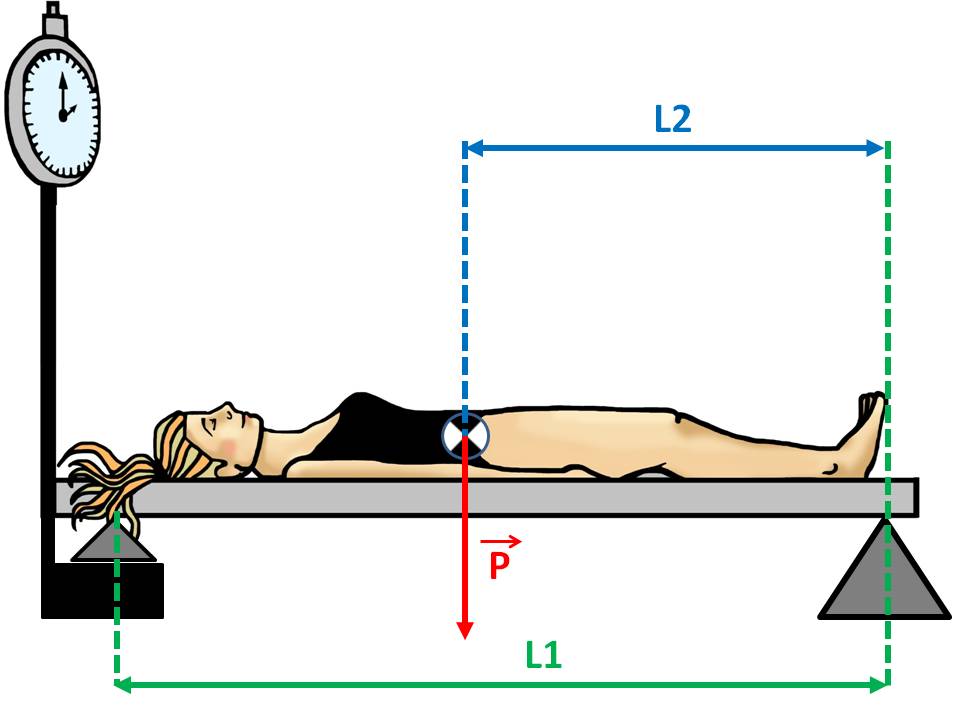
Mètode per al càlcul del CDG de Reynolds i Lovett. P = pes del subjecte; L1 = longitud entre els punts de suport; L2 = alçada del CDG.
Per calcular l’altura del CDG des dels peus, s’ha de conèixer en primer lloc el pes parcial del subjecte. Per a això es resta al pes parcial persona-taula el de la taula sola. El pes parcial es multiplica per la distància d’un punt de suport a l’altre i es divideix entre el pes de l’individu. Aquesta serà l’altura del CDG.
La fórmula seria:
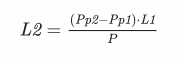
Fórmula per calcular l’altura del CDG. P = pes del subjecte; PP1 = pes parcial de la taula; PP2 = pes parcial del sistema persona-taula; L = longitud entre els punts de suport; l = altura del CDG.
Aquest mateix sistema es pot utilitzar per conèixer el tall transversal del CDG en altres posicions que reprodueixin gestos tècnics esportius o en posició bípeda.
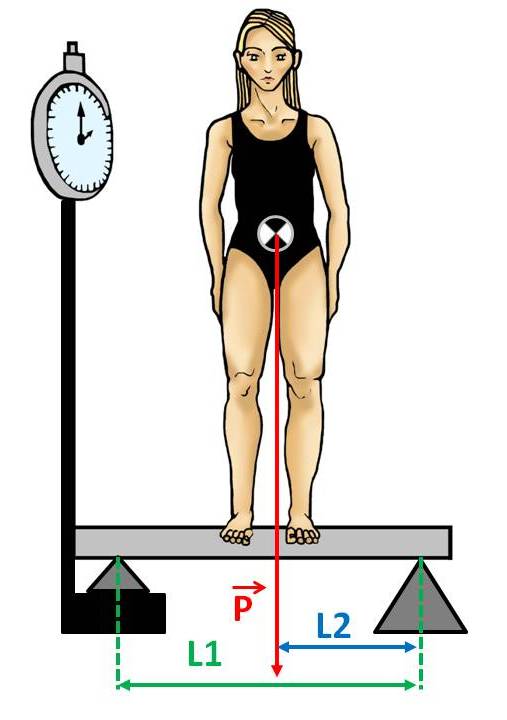
Mètode per al càlcul del CDG de Reynolds i Lovett. P = pes del subjecte; L1 = longitud entre els punts de suport; L2 = distància del punt de suport més allunyat de la bàscula a CDG.
Aprèn més
Podeu donar una ullada a aquesta pràctica que he trobat de la Facultad de Ciencias del Deporte de Toledo pel mateix Xavier Aguado fent clic aquí. De fet, sembla que hi ha un bon grapat d’apunts que poden complementar bé aquesta sèrie d’entrades sobre biomecànica 😉
L’equilibri i la biomecànica esportiva
El CDG s’utilitza en biomecànica per simplificar el moviment d’un cos i les forces que actuen sobre ell (López, 2008). Concretament s’aplica per als següents casos (Aguado, 1993):
- Interpretar les situacions d’equilibri.
- Descriure les trajectòries dels esportistes en el terreny de joc. En aquests casos es simplifica en el CDG els desplaçaments globals dels subjectes d’estudi.
- Analitzar els girs en l’aire, ja que es realitzen al voltant del CDG.
- Descriure la trajectòria de vol durant els salts. La trajectòria del CDG roman invariable una vegada que es perd el contacte amb el terra, malgrat els moviments dels segments corporals que es realitzin per l’aire.
A la pràctica esportiva es realitzen continus ajustaments de reequilibri, unes vegades per guanyar punts (com és en el cas de les modalitats artístiques), altres per no perdre’ls (com passa en Judo), altres per poder executar una tècnica de forma més eficient (com en el tir amb arc) i també en altres per evitar lesions (com passa en el futbol).
Una de les estratègia més senzilles és la de augmentar la BDS. Amb això s’evita que la LDG surti fora de la BDS el que significaria una caiguda gairebé segura. La BDS ha d’ampliar-se en el mateix sentit que la força desestabilitzadora. En cas contrari no tindria sentit. Si un subjecte està amb els dos peus junts, si rep una empenta de darrere cap endavant, haurà d’avançar un peu per evitar caure de morros.
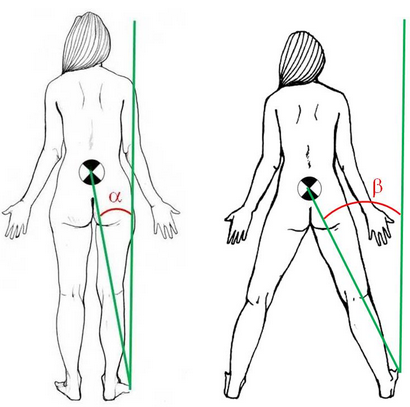
A l’augmentar la base de sustentació també augmenta l’angle de caiguda, per tant l’estabilitat serà més gran (β > α).
Una altra estratègia senzilla és la de reduir l’alçada del CDG. Amb això, tot i mantenir la mateixa BDS, s’aconsegueix augmentar l’angle de caiguda i per tant millora l’estabilitat del subjecte.
Efectuar moviments compensatoris amb les extremitats són també estratègies re-equilibradores molt utilitzades (Aguado, 1993). Aquests moviments són especialment aplicables quan el subjecte es troba a certa alçada de terra, perquè el cos tendiria a girar sobre el CDG. En aquests casos s’aplica el principi d’acció-reacció de Newton.
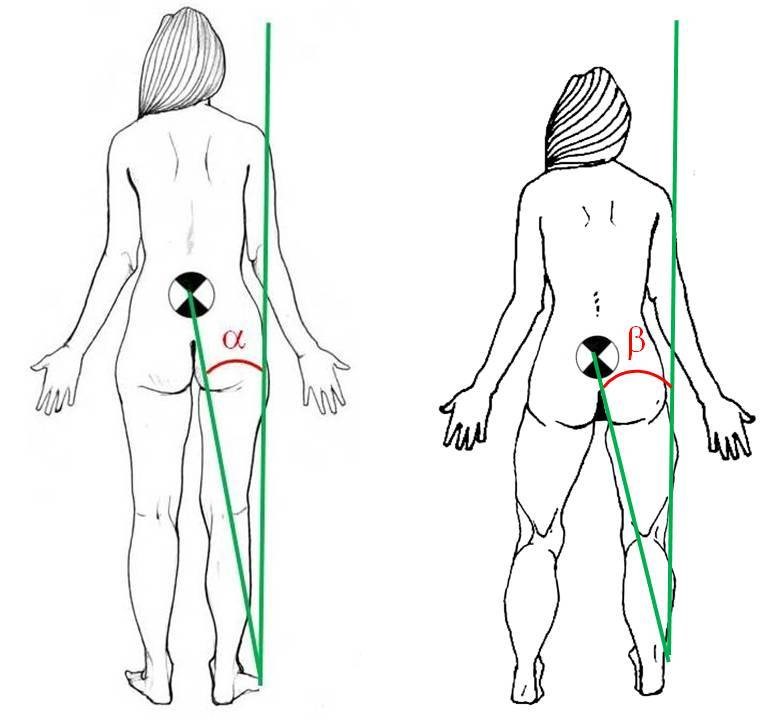
En reduir l’alçada del CDG augmenta l’angle de caiguda, per tant l’estabilitat serà més gran (β > α).
Per exemple, quan una gimnasta està sobre la barra d’equilibri i davant d’una desestabilització lateral, desplaça una cama, tronc o braços cap al costat de caiguda. D’aquesta manera la força de reacció compensa el desequilibri cap a la zona contrària tornant a re-equilibrar-se.
Un altre exemple de compensació amb les extremitats serien els moviments aspats. Són girs que es realitzen amb els braços davant d’una des-estabilització en el pla frontal, ja sigui cap endavant o cap al darrere. L’exemple més clar és quan una persona situada a la vora de la piscina és lleugerament empesa cap a l’aigua. Amb aquests girs en sentit contrari al desequilibri pot evitar la seva caiguda.
De vegades, en els esports d’esllavissades es recorre a una força externa per re-equilibrar. Quan s’esquia se sol usar els bastons per mantenir l’estabilitat. De la mateixa manera passa amb la vela en windsurf.

En kitesurf l’esportista manté la seva estabilitat per la subjecció a l’estel, tant amb el braç com amb l’arnès.
Per finalitzar la unitat, en aquest vídeo de l’obra Violoncel, de Nacho Duato (Companyia Nacional de Dansa) interpretada per Àfrica Guzmán i Alejandro Álvarez, s’aprecia com la ballarina recorre a les diferents estratègies re-equilibradores comentades en aquest apartat.
En resum
La força és una magnitud vectorial definida com la causa capaç de modificar l’estat de repòs o de moviment d’un cos o de deformar-lo. Tot cos exerceix una força en relació amb l’acceleració gravitatòria. Aquesta magnitud s’anomena pes i no s’ha de confondre amb la massa d’un cos, que és una magnitud escalar que representa la quantitat de matèria que té un cos.
Les forces poden classificar-se en forces de contacte i forces sense contacte (Brancazio, 1984). Alegre (2008) les divideix en forces de reacció, ascensional, de fregament, de resistència, de sustentació centrífuga i centrípeta.
Respecte a la Força, Newton va establir tres lleis:
- Primera Llei: tot cos romandrà en estat de repòs o en moviment rectilini uniforme mentre no hi hagi forces externes que actuen sobre ell.
- Segona Llei: quan una força actua sobre un cos, aquest experimenta una acceleració proporcional a aquesta força que tindrà la seva mateixa direcció i sentit.
- Tercera Llei: quan un cos exerceix una força d’acció sobre un altre, aquest reacciona amb una força del mateix mòdul i direcció però de sentit contrari.
De la segona llei de Newton es pot deduir dos conceptes cinètics. L’impuls mecànic que seria la variació de la força exercida sobre un cos en funció del temps que està actuant, i la quantitat de moviment o el producte de la massa d’un cos per la variació de la velocitat.
D’altra banda, l’equilibri es defineix com l’estat d’un cos quan les forces oposades que obren en ell es compensen destruint-se mútuament. Això no vol dir que no hi hagi forces o moments de forces actuant, sinó que els vectors s’anul·len entre si.
En biomecànica, l’equilibri es vincula al manteniment d’una posició al llarg del temps sense perdre-la. La base de sustentació (BDS) es defineix com l’àrea d’un polígon format per les arestes que uneixen els punts extrems amb el qual es recolza o sosté un cos. Com més gran és la BDS més estabilitat té el sistema.
Els equilibris es classifiquen en: equilibri estable, equilibri inestable, equilibri indiferent i equilibri hiperestable.
El centre de gravetat (CDG) és el lloc en el qual es concentraria tot el pes del cos si fos comprimit des de totes direccions. Seria el punt on conflueix la força resultant del pes de tots els segments d’un cos. Els cossos normalment es poden dividir en segments, de manera que cada un té el seu particular CDG. La sumatòria de tots aquests punts convergiria al CDG del cos.
La línia vertical imaginària que uneix el CDG amb el terra es denomina línia de gravetat (LDG). Si la projecció de la LDG s’ubica dins de la BDS el cos estarà estable, en canvi si es projecta fos el cos tendirà a caure. El centre de masses (CDM) és el punt mig on es concentraria tota la massa d’un cos. Mentre que el CDG fa referència al pes d’un cos.
Hi ha dos tipus de mètodes per calcular el CDG: mètodes directes i mètodes indirectes. Els mètodes directes són aquells que es realitzen sobre el cos que es vol conèixer el seu CDG. Els presentats en aquesta unitat són el mètode directe de la plomada i el mètode directe de Reynolds i Lovett.
El CDG s’utilitza en biomecànica per simplificar el moviment d’un cos i les forces que actuen sobre ell. A la pràctica esportiva es realitzen continus ajustaments del CDG: augmentant la BDS, reduint l’altura del CDG, efectuant moviments compensatoris amb les extremitats, moviments aspats amb els braços o recórrer a una força externa per re-equilibrar-se.













